In this study, we will investigate the performance and efficient of the transpose matrix using row-majors and column-majors access.
- Matrix Transpose performance
The following code helps to compute the matrix transpose of n x n matrix B=A^T.
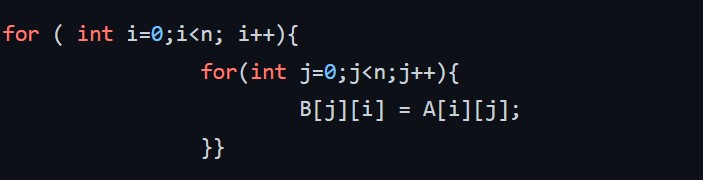
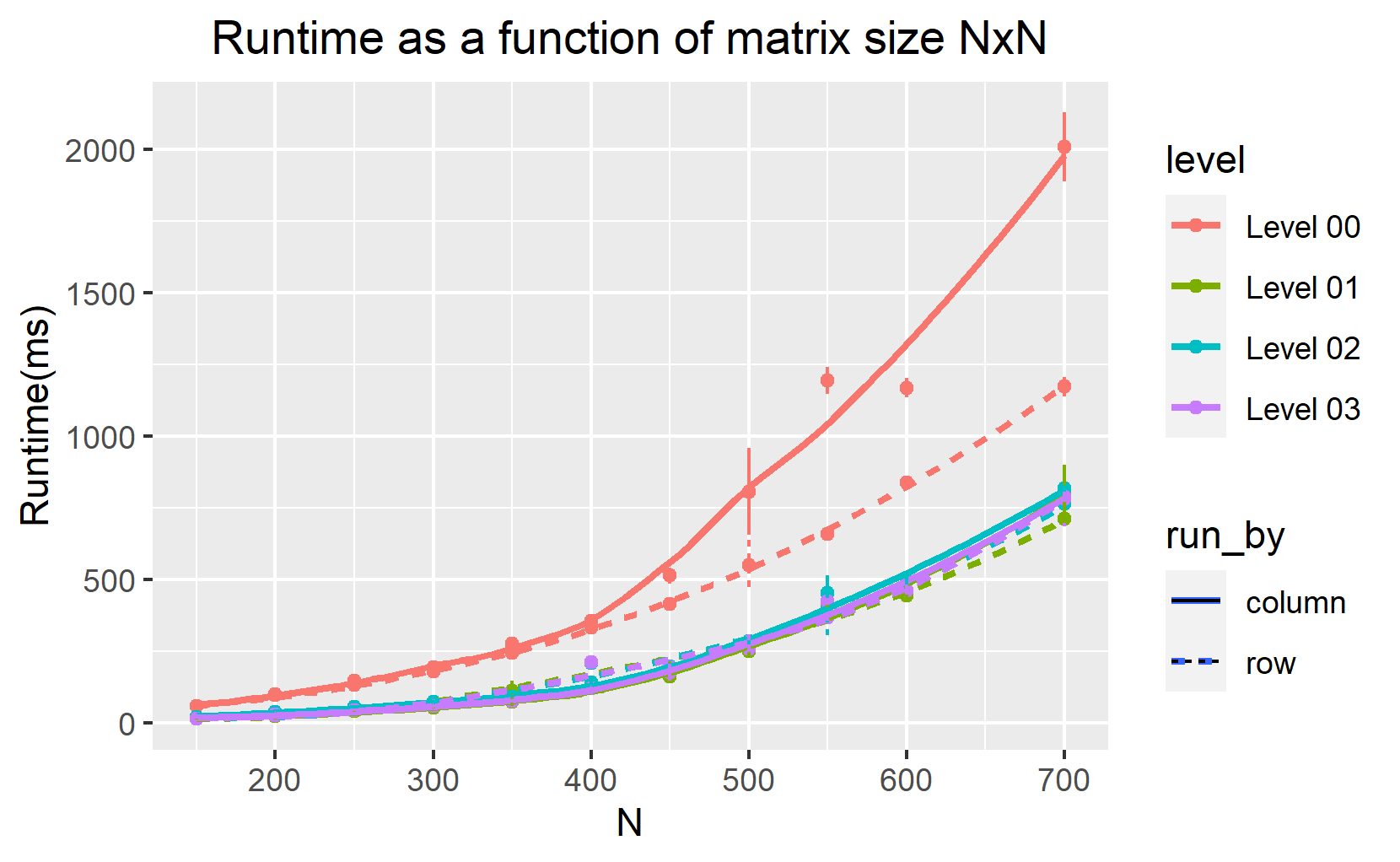
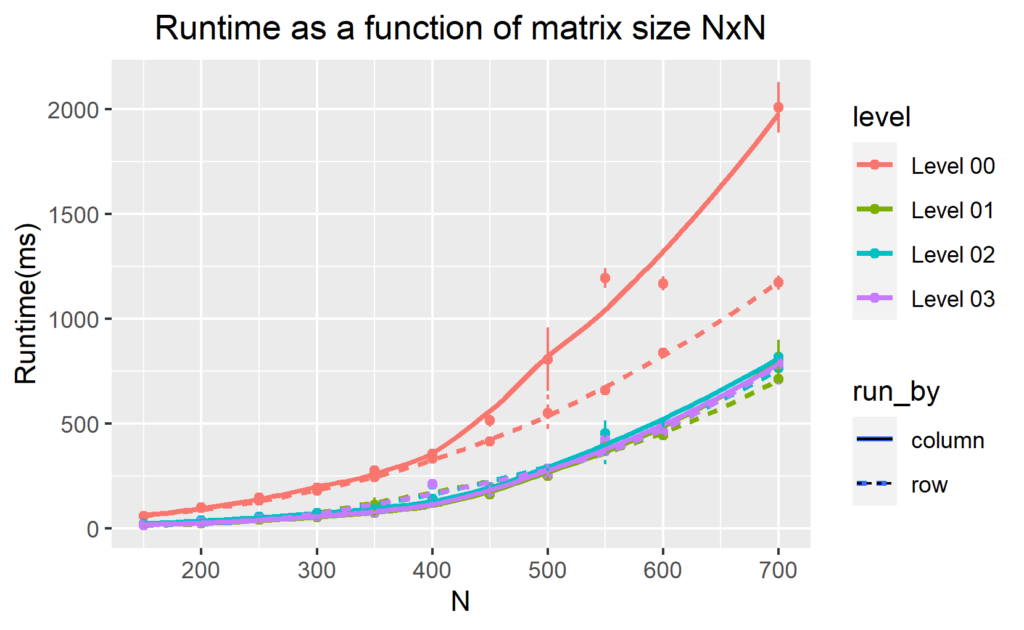
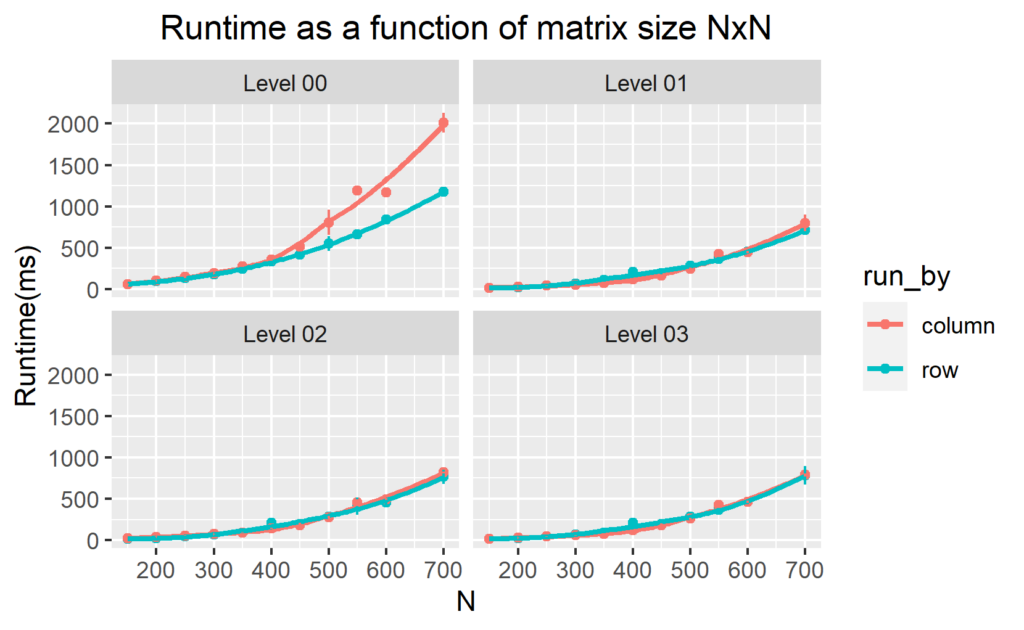
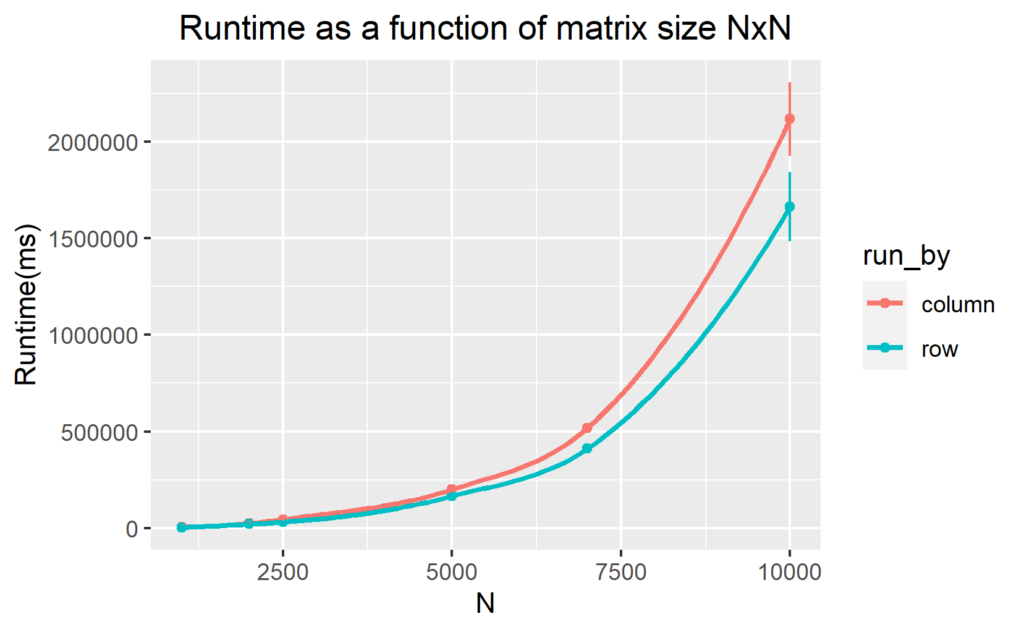
I interchanged the loops over i and j (loop over i become inner loop and loop over j become the outer loop:column-wise manner) to measure the computation time for the different n values. I them display the computation time as a function of n (figure 1 and 2). To speed up the runtime of the code, we perform different levels of optimization during compilation from none (-O0) through to (-O3) . Figure 1 and 2 below show our results.
Discusion
Figure 1 and figure 2 show that for level -O0, the most efficient code to compute the transpose of multiple matrix dimensional arrays is when using row-major access even for the higher level of optimization. We find that the row-major access for large two-dimensional arrays is approximately 2 times faster than the column-major access. This is because row-major access explores the memory non-sequentially (let’s explore this in detail in the next section).
2. Issues with Matrix Representation
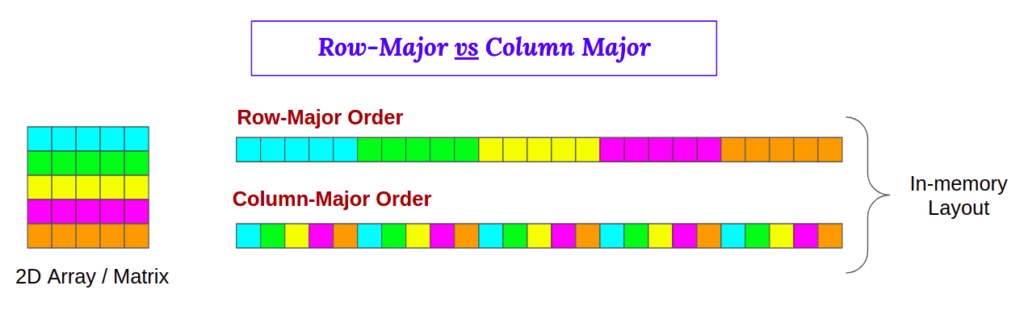
We need to understand how data is stored and accessed in the memory to understand our results. Matrices in C/C++ are stored in a row-major layout (see figure 3) in the RAM, but in column-major order in Fortran. The cache memory mapping is give by the figure 4.
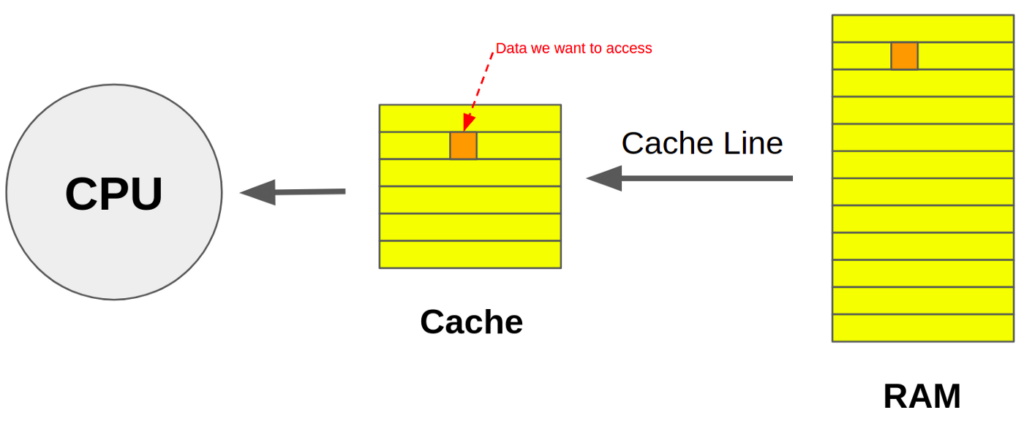
When the CPU needs to access data, the system first checks to see if it is in the cache. This is called cache hit If the the data was discovered in the cache. As a result, data can be accessed more quickly (which is trivial since it takes longer to load data from RAM). When data cannot be loaded from the cache and must be loaded from memory, this is called a cache miss. Our findings can now be easily analyzed.
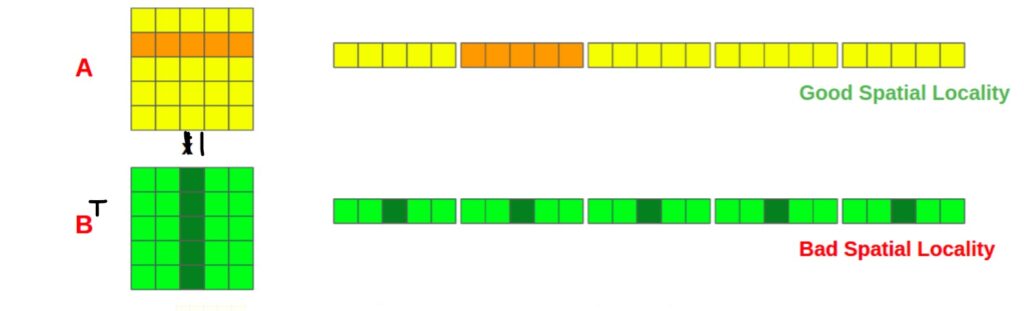
We require access to the entire second column of matrix B as well as the entire second row of matrix A. Looking at the in-memory layout in the diagram, you can see that accessing the second row of matrix A provides good spatial locality because all of the data we require are in a single cache line. In matrix B, however, we must access different cache lines for each column value, resulting in a higher cache miss rate. So iterating the matrix column-wise isn’t optimal and should be avoided if possible. Additionally, transposing the matrix should reduce L1 cache misses when using row-major access.
A will be scanned n times, so if the cache cannot hold a whole row of elements, there will be nxn/L caches misses. When n is large enough, B is scanned with stride of n for each iteration, leading to nxn cache misses. In row-major, the total number of cache misses is nxn + nx n/L. The access latency increases with each cache miss, which slows down transposition. Using the following command, we can calculate the cache miss rate for N=700; valgrind –tool=cachegrind ./cache
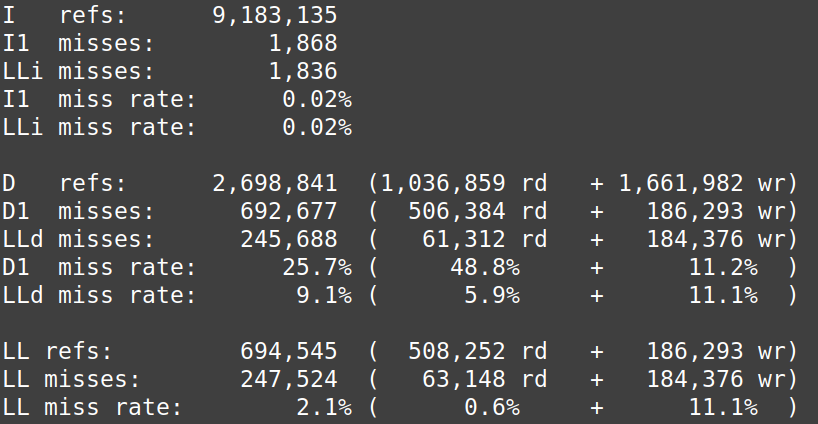
My computer’s L1 cache is 64 bit (I checked using getconf LEVEL1_DCACHE_LINESIZE). Since the 2D dimension array we declare is of double type (8 bits, so L=8 elements), the theoretical total number of missing reading caches in a L1D cache line for column-major access is 551 250, which is slightly lower than the experimental result. There are more reading cache misses than writing cache misses for the row-major access. We conclude, based on figure 1, that reading cache miss costs more than writing cache miss when transposing matrices.
Cachegrind simulates the first level and last level caches. An L1 miss typically costs around 10 cycles, and an LL cache miss can cost 200 cycles. The static shows us that the D1 miss rate for reading is 48.8% and 11.2% for write miss in column-major access. In column row-major access, the D1 miss rate for reading is 7.5% and 37.0 % for write miss.
3. Array Allocation and stack
There is a limit to the array allocation when we use the automatic storage declaration to get a matrix placed in contiguous memory. We got a segmentation fault when N exceeded 700. It corresponds to 700^2 x 8 = 3.8 KB in memory. Because our stack’s maximum size is 16KB, the operating system allocates a maximum memory stack to our process. We declared the matrix as static to test our operation on a very large matrix. This help to have a matrix with with maximum size 10000 x 10000. We still have the same interpretation as in subsection 1.1.
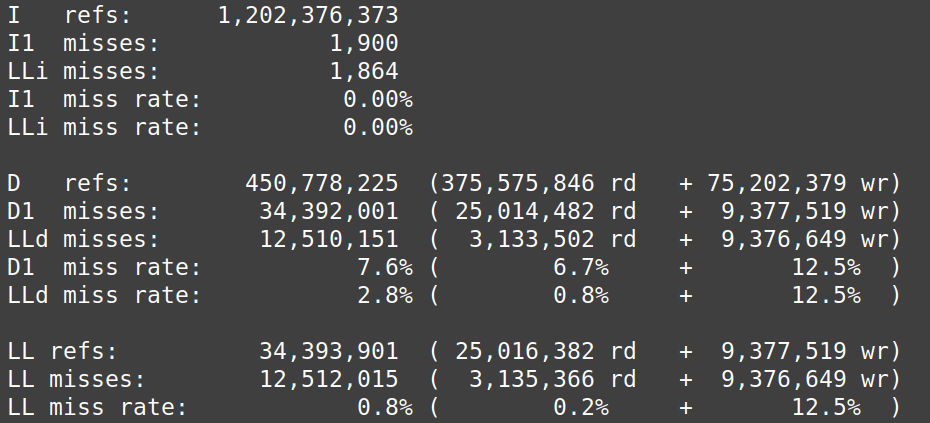

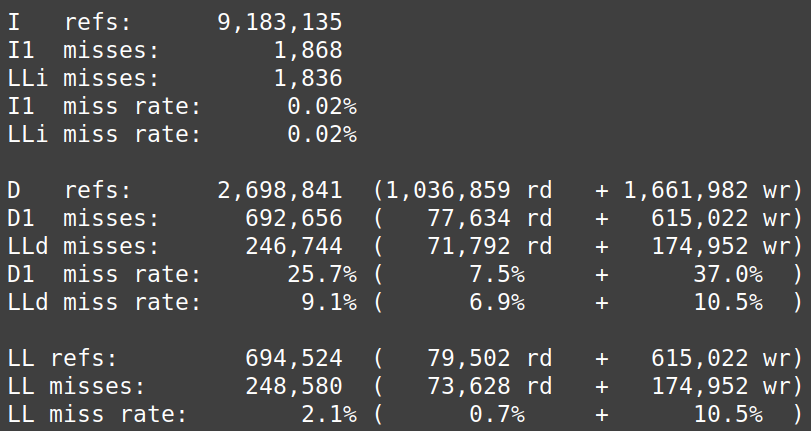
According to the Cachegrind simulation figure 9 and 10, row-major access has the lowest reading cache miss rate (0.8%) and writing cache miss rate (41.6%), however column-major access has the highest cache miss rate and lowest write miss rate.

I am a master’s student in Data Science and Scientific Computing.